Normal Attention Computation
\[S = QK^{T} \in R^{N \times N}\]
\[P = \text{softmax}(S) \in R^{N \times N}\]
\[O = PV \in R^{N \times D}\]
where \(N\) is sequence length and \(D\) is dimension.
Flash Attention
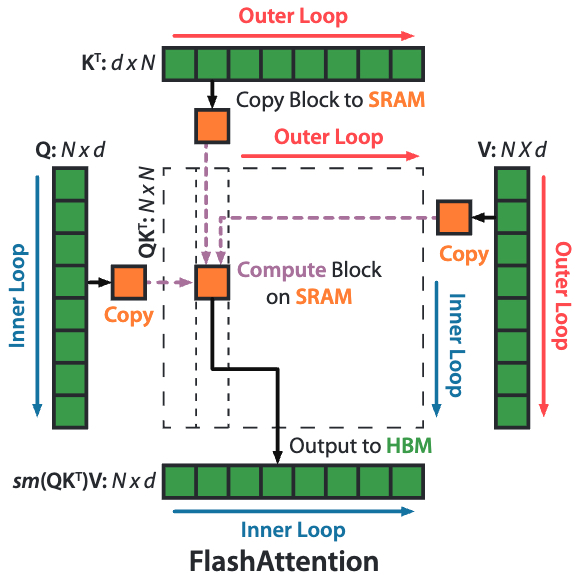
分块 softmax 算法
\[a = [0.1, 0.2, 0.3, 0.4] = [a_1, a_2];\ m(a_1) = 0.2;\ m(a_2) = 0.4;\ m(a) = 0.4\]
\[f(a_1) = [e^{0.1-0.2}, e^{0.2-0.2}];\ l(a_1) = \sum f(a_1)\]
\[f(a_2) = [e^{0.3-0.4}, e^{0.4-0.4}]; l(a_2) = \sum f(a_2)\]
\[f(a) = [e^{0.2-0.4}f(a_1), e^{0.4-0.4}f(a_2)]\]
\[l(a) = e^{0.2-0.4} l(a_1) + e^{0.4-0.4} l(a_2) \]
\[\text{softmax}(a) = \frac{f(a)}{l(a)}\]