Time
Computation
A deep learning model is effectively a bunch of matrix multiplications, each composed of floating-point multiplication and addition ‘operations’ (FLOPs). Our accelerator speed determines how long these take to compute:
\(T_{math} = \text{Computation_FLOPs} / \text{Accelerator_FLOPs/s}\)
例如,NVIDIA H100 大约能达到 9.89e14 bfloat16 FLOPs/s 的性能,而 TPU v6e 则为 9.1e14 FLOPs/s。这意味着在 H100 上执行 1e12 FLOPs 大约需要 1e12 / 9.89e14 = 1.01 毫秒,在 TPU v6e 上则需要 1e12 / 9.1e14 = 1.1 毫秒。
Communication within a chip
在 Accelerator 内部,Tensor 需要在片上存储器(HBM)和 Tensor Core 之间进行传输。这种连接的带宽被称为“HBM 带宽”。在 H100 上,这个带宽大约是 3.35 TB/s,而在 TPU v6e 上,大约是 1.6 TB/s。
Communication between chips
当我们把一个模型分布式部署到多个加速器上时,张量(数据)经常需要在它们之间进行传输。在我们的硬件上,通常有几种实现这种传输的选项(ICI、DCN 和 PCIe),每种都有不同的带宽。
不论是对于 inner chip,还是 intra chips,可以通过以下公式衡量时间:
\[T_{comms} = \frac{\text{Communication_Bytes}}{\text{Network/Memory_Bandwidth_Bytes/s}}\]
计算访存比(Intensity):

Intensity(Accelerator) TPU 达到其峰值 FLOPs/s 时的算术强度。对于 TPU v5e MXU,这大约是 240 FLOPs/B,因为 TPU 每秒可以执行 1.97e14 FLOPs 并从 HBM 加载 8.2e11 字节/秒。
如果一个算子的计算强度低于 240 FLOPs/B,它将进入访存瓶颈,否则会进入计算瓶颈。
Self Dot Product
对于两个 vector
的内积:x * y: bf16[N] * bf16[N] → bf16[1],我们需要将
x 和 y
加载到内存中进行计算,每个 vector 有 2N
的数据需要加载,进行 N 次乘法和 N-1 次加法:
\[Intensity(dot product) = \frac{N + N - 1}{2N + 2N} → \frac{1}{2}\]
当 \(N → \inf\),这个计算访存比为 0.5,每加载一个字节的数据进行 0.5 次浮点计算,这意味着该阶段的通信开销远远大于计算开销。
Roofline
Matrix Gemm
对于以下配置:
| array | shape |
|---|---|
| \(x\) | \([P]\) |
| \(y\) | \([P]\) |
| \(A\) | \([N P]\) |
| \(B\) | \([P M]\) |
- 两个向量 \(x \cdot y\) 的 点积 需要 \(P\) 次加法和乘法,总计 \(2P\) 次浮点运算。
- 矩阵-向量积 \(Ax\) 需要对 \(A\) 的行进行 \(N\) 次点积,总计 \(2NP\) 次浮点运算。
- 矩阵-矩阵积 \(AB\) 需要对 \(B\) 的每列进行 \(M\) 次矩阵-向量积,总计 \(2NPM\) 次浮点运算。
- 通常,如果我们有两个 高维数组 \(C\) 和 \(D\),其中一些维度是 CONTRACTING 维度,一些是 Batching维度。(例如,\(C[GHIJKL]\),\(D[GHMNKL]\)),那么这种收缩的浮点运算成本是 \(C\) 和 \(D\) 所有维度的乘积的两倍,其中批处理和收缩维度只计算一次(例如,\(2GHIJMNKL\))。请注意,一个维度只有在两个乘数中都出现时才进行批处理。(另请注意,如果没有收缩维度,则因子2不适用,这只是一个元素级乘积。)
Batching Dimension
Contracting Dimension
Non Batching and Non Contracting Dimension
Transformer
首先给出一系列 dimension 的符号表示:
| symbol | dimension |
|---|---|
| \(B\) | batch size |
| \(L\) | number of layers |
| \(T\) | sequence length (query) |
| \(S\) | sequence length (key value) |
| \(V\) | vocab |
| \(D\) | \(d_{model}\), embedding dimension |
| \(F\) | MLP intermidiate dimension |
| \(H\) | attention head dimension |
| \(N\) | number of query heads |
| \(K\) | number of key/value heads |
| \(G\) | q heads per kv head = \(N // K\) |
需要注意以下几点:
embedding size 和 hidden size
两者在实践中一般相同,但是却是不同的概念,embedding size 指的是对 token 进行 embed 后的维度。 hidden size 指的是 Q/K/V 的维度
Q 和 K/V 的维度
Q/K/V 的维度在实践中一般相同,但是在理论上可以不同,对于多头注意力,q 的维度是 NH,k/v 的维度是 KH。
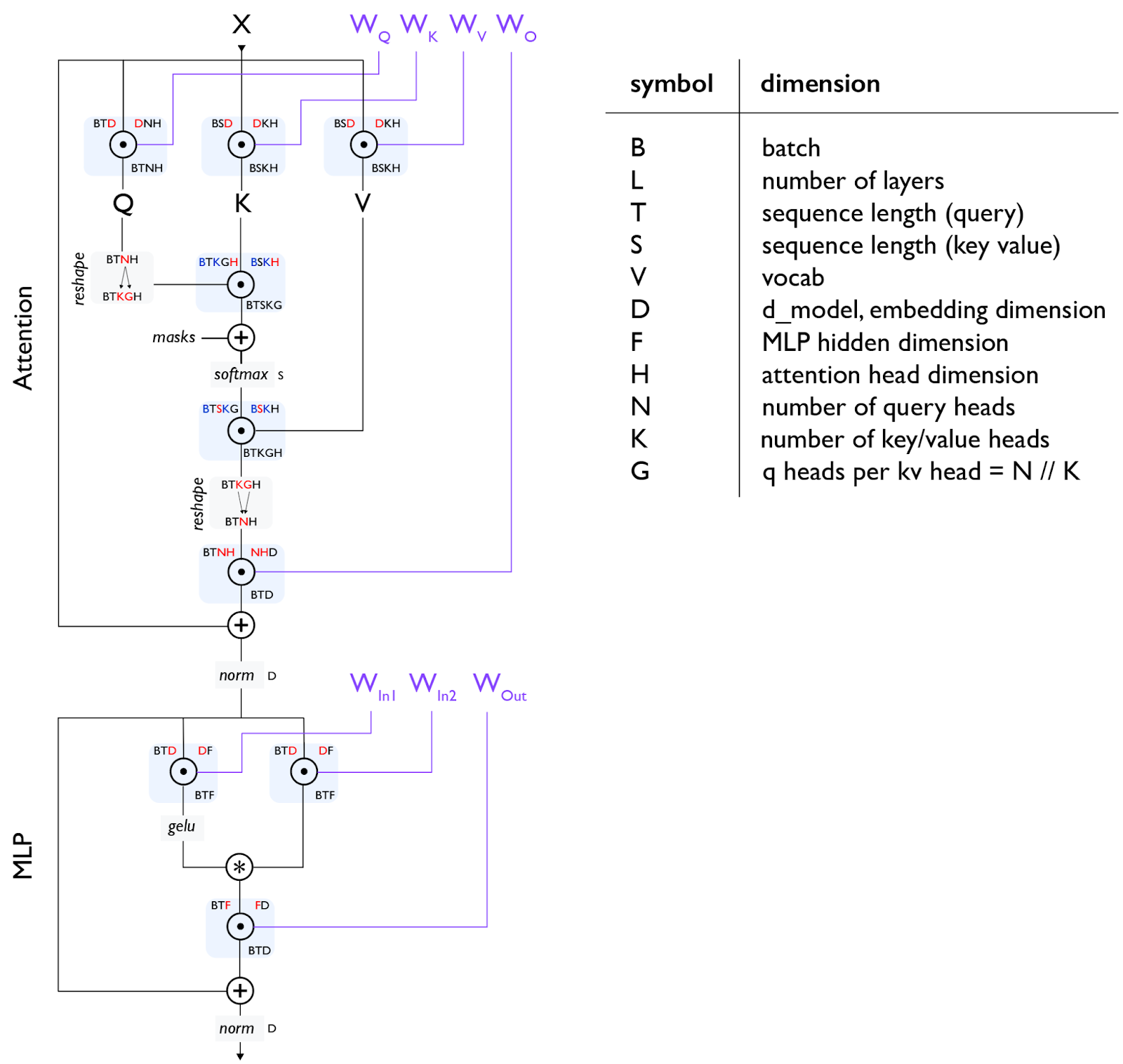
为什么要区分 K/N
- 对于 MHA,K 和 N 相同
- 对于 MQA,K = 1
- 对于 GQA,N 是 K 的整数倍,G = N / K
gating einsum
这是一段关于“门控爱因斯坦求和”(gating einsum)的解释,以下是翻译内容:
我们将上投影矩阵分成两个矩阵(上面的 \(W\_{In1}\) 和 \(W\_{In2}\)),它们的输出进行逐元素相乘,作为一种“门控函数”。并非所有大型语言模型(LLM)都使用这种方法,所以有时你会看到一个单独的 \(W\_{In}\) 矩阵,并且总的多层感知器(MLP)参数计数是 2DF 而不是 3DF。通常在这种情况下,D 和 F 会按比例放大,以保持参数计数与三个矩阵的情况相同。尽管如此,Llama、DeepSeek 和许多其他模型都使用了某种形式的门控爱因斯坦求和。
MLPs
Gated MLP
\[ A = \sigma(X W_{in1}) \odot (X W_{in2}) \]
解释:
- \(W_{in1}, W_{in2}\) 都是从输入维度 \(D\) 投影到扩展维度 \(F\) 的两个不同矩阵
- 第一个投影 \(X W_{in1}\) 通过 sigmoid 激活变成门控值
- 第二个投影 \(X W_{in2}\) 作为被门控的主流路径
- 二者逐元素相乘之后再通过 \(W_{out}\) 降维
这种结构比标准 MLP 更灵活,最早用于 GLU,也出现在 Gated MLP, SwiGLU, GeGLU 等设计中。
| operation | train FLOPs | params |
|---|---|---|
| \(A[B, T, \textcolor{red}{D}] \cdot W_{in1}[\textcolor{red}{D}, F]\) | \(6BTDF\) | \(DF\) |
| \(A[B, T, \textcolor{red}{D}] \cdot W_{in2}[\textcolor{red}{D}, F]\) | \(6BTDF\) | \(DF\) |
| \(\sigma(A_{in1})[B, T, F] * A_{in2}[B, T, F]\) | \(O(BTF)\) | |
| \(A[B, T, F] \cdot W_{out}[F, D]\) | \(6BTDF\) | \(DF\) |
| \(\approx 18BTDF\) | \(3DF\) |
Attention
| operation | train FLOPs | params |
|---|---|---|
| \(A[B, T, \textcolor{red}{D}] \cdot W_Q[\textcolor{red}{D}, N, H]\) | \(6BTDNH\) | \(DNH\) |
| \(A[B, T, \textcolor{red}{D}] \cdot W_K[\textcolor{red}{D}, K, H]\) | \(6BTDKH\) | \(DKH\) |
| \(A[B, T, \textcolor{red}{D}] \cdot W_V[\textcolor{red}{D}, K, H]\) | \(6BTDKH\) | \(DKH\) |
| \(A[B, T, N, H] \cdot W_O[N, H, D]\) | \(6BTDNH\) | \(DNH\) |
| \(\mathbf{12BTD(N + K)H}\) | \(\mathbf{2D(N + K)H}\) |
| operation | train FLOPs |
|---|---|
| \(Q[B, T, \textcolor{blue}{K}, G, \textcolor{red}{H}] \cdot K[B, S, \textcolor{blue}{K}, \textcolor{red}{H}]\) | \(6BTSKGH = 6BTSNH\) |
| \(\text{softmax}_S\quad L[B, T, S, K, G]\) | \(O(BTSKG) = O(BTSN)\) |
| \(S[B, T, \textcolor{red}{S}, \textcolor{blue}{K}, G] \cdot V[B, \textcolor{red}{S}, \textcolor{blue}{K}, H]\) | \(6BTSKGH = 6BTSNH\) |
| \(\approx 12BTSNH = 12BT^2NH\) |
attn & gemm
Let’s consider all the gemm operations (\(A \cdot B\)):
| B Name | A | B | Param | FLOPs |
|---|---|---|---|---|
| \(W_{Q}\) | \([B, D]\) | \([D, N, H]\) | \(DNH\) | \(2BDNH\) |
| \(W_{K}, W_{V}\) | \([B, D]\) | \([D, K, H]\) | \(DKH\) | \(2BDKH\) |
| \(W_{O}\) | \([B, N, H]\) | \([N, H, D]\) | \(DNH\) | \(2BDNH\) |
| \(W_{in1}, W_{in2}\) | \([B, D]\) | \([D, F]\) | \(DF\) | \(2BDF\) |
| \(W_{down}\) | \([B, F]\) | \([F, D]\) | \(DF\) | \(2BDF\) |
Let’s consider the attention operation:
| Type | A | B | FLOPs |
|---|---|---|---|
| \(QK^T\) | Q \([B, T, N, H]\) | K \([B, S, K, H]\) | \(2BTSNH\) |
对于 prefill 阶段,T=S=prompt tokens数量,QK 的计算量为 \(2BT^2 NH\),随着上下文二次增长。
对于 decode 阶段,T=1,S=上下文长度,QK 的计算量为 \(2BSNH\),随着上下文长度线性增长。
| Phase | Type | A | B | FLOPs |
|---|---|---|---|---|
| prefill | Softmax(\(QK^T\)) * V | \([B, T, N, H]\) | \(V\) \([B, T, K, H]\) | \(2BT^{2}NH\) |
| decode | Softmax(\(QK^T\)) * V | \([B, 1, N, H]\) | \(V\) \([B, S, K, H]\) | \(2BSNH\) |
对于训练
Suppose \(F = 4D\),\(N = K\):
\[\frac{\text{attention}}{\text{gemm}} = \frac{12BT^2NH}{18BTDF + 24BTDNH} = \frac{12BT^2D}{4 * 18BTD^2 + 24BTD^2} = \frac{12BT^2D}{96BTD^2} = \frac{T}{8D}\]
所以只有当 \(T > 8D\) 的时候 attention 的计算量才会超过 gemm,假设 hidden size = 8K,只有上下文长度达到 64k 时 attention 计算量才会超过 gemm。
对于推理
Suppose \(F=5D\),\(N=K\):
\[\frac{\text{attention}}{\text{gemm}} = \frac{8BD^2 + 2BSD}{6BDF} = \frac{8D + 2S}{24D}\]
当上下文长度 \(S > 8D\) 时,attention 阶段的计算量会超过 MLP。
general rule
如果上下文比较短,然后忽略 attention 阶段的 self dot product 的计算量的话,那么计算量可以近似为:
\[ \begin{align*} (18BTDF + 12BTD(N+K)H)L = 6 * BT * (3DF + 2D(N+K)H)L \\ = 6 * \text{num tokens} * \text{parameter count} \end{align*} \]
这引出了一个著名的经验法则,用于估算密集型 Transformer 的浮点运算数(FLOP),同时忽略了注意力机制的浮点运算。 (去嵌入(Unembedding)是另一个简单的矩阵乘法,有 \(6BSDV\) 浮点运算和 \(DV\) 参数,也遵循相同的经验法则。)