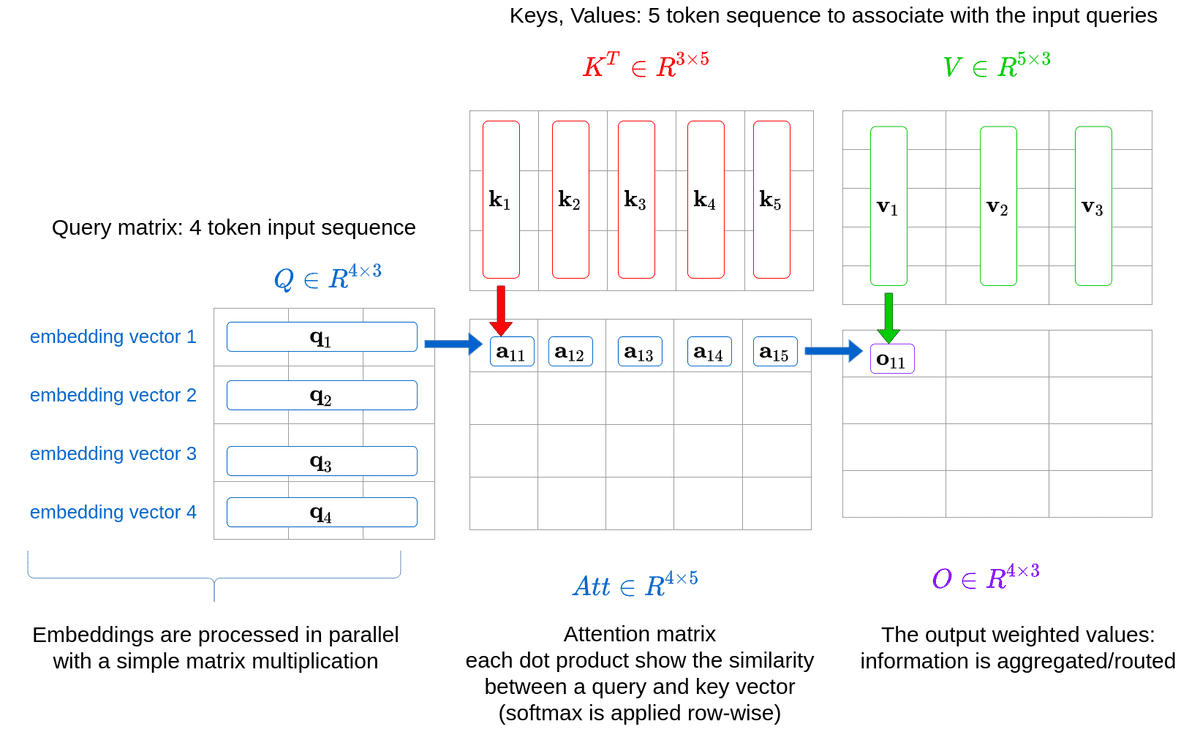
MHA
输入为矩阵 \(X \in \mathbb{R}^{L \times d_{\text{model}}}\),长度为 \(L\),模型维度为 \(d_{\text{model}}\)。
我们有:
- \(h\):attention head 的数量
- \(d_k = d_v = d_{\text{model}} / h\)
每个 head 有独立的投影:
\[ Q_i = X W_i^Q,\quad K_i = X W_i^K,\quad V_i = X W_i^V,\quad i = 1, \dots, h \]
每个 head 的 attention:
\[ \text{head}_i = \text{softmax}\left( \frac{Q_i K_i^\top}{\sqrt{d_k}} \right) V_i \]
最后拼接并映射输出:
\[ \text{MHA}(X) = \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^O \]
MQA
MQA:Multi-Query Attention(多查询注意力)
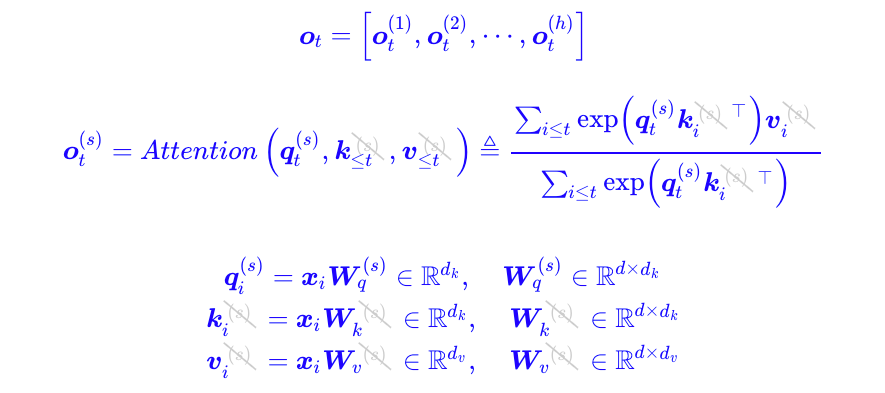
核心区别:所有 head 共享同一个 K 和 V。
我们仍然有:
- \(Q_i = X W_i^Q \quad (i = 1, \dots, h)\)
- 但所有 head 使用同一组: \[ K = X W^K,\quad V = X W^V \]
那么每个 head 的 attention 变成:
\[ \text{head}_i = \text{softmax}\left( \frac{Q_i K^\top}{\sqrt{d_k}} \right) V \]
最后再拼接:
\[ \text{MQA}(X) = \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^O \]
GQA
GQA:Grouped Query Attention(分组查询注意力)
GQA 就是对 hidden dimension 进行分组,组内使用相同的 K/V,相当于采取了 MHA 和 MQA 的一个这种方案,对于每一组,实际上是使用 MQA。
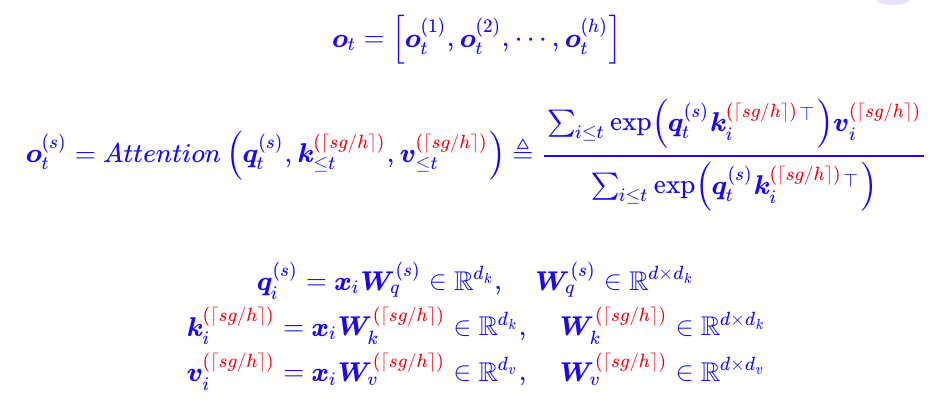
假设:
- \(h\):总 head 数
- \(g\):K/V 分组数(每组共享一个 K/V)
- \(h_g = h / g\):每组中的 head 数
我们有:
- 对每组 \(j = 1, \dots, g\),生成: \[ K_j = X W_j^K,\quad V_j = X W_j^V \]
- 每个 head \(i\) 属于某组 \(j = \lfloor i / h_g \rfloor\),该 head 用: \[ Q_i = X W_i^Q,\quad K_j,\quad V_j \]
对应 attention 计算为:
\[ \text{head}_i = \text{softmax}\left( \frac{Q_i K_j^\top}{\sqrt{d_k}} \right) V_j \]
最后一样拼接:
\[ \text{GQA}(X) = \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^O \]
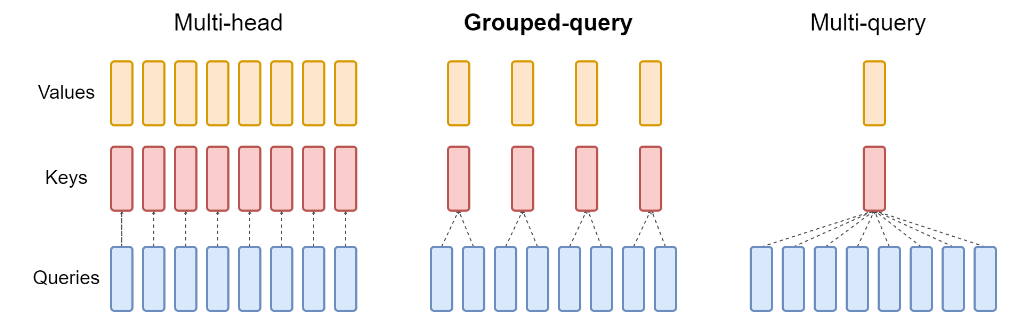
| \(Q_i\) | \(K_i, V_i\) | 说明 | |
|---|---|---|---|
| MHA | 独立 | 独立 | 每个 head 有自己的一套 K/V |
| MQA | 独立 | 所有 head 共用一个 \(K, V\) | 显存最省,但表达力略差 |
| GQA | 独立 | 每组共享 \(K_j, V_j\)(共 \(g\) 组) | 折中方案,性能和表达力均衡 |
Code
Attention
\(Q, K, V = XW\)
\(Attention(Q, K, V) = \text{Softmax}(\frac{Q K^{T}}{\sqrt{d_k}}) V\)
\(Output = Attention(Q, K, V) W_{O}\)
import numpy as np
import torch
from einops import rearrange
from torch import nn
class SelfAttentionAISummer(nn.Module):
def __init__(self, dim):
super().__init__()
self.to_qvk = nn.Linear(dim, dim * 3, bias=False)
self.scale_factor = dim ** -0.5 # 1/np.sqrt(dim)
def forward(self, x, mask=None):
assert x.dim() == 3, '3D tensor must be provided'
qkv = self.to_qvk(x) # [batch, tokens, dim*3 ]
# decomposition to q,v,k
# rearrange tensor to [3, batch, tokens, dim] and cast to tuple
q, k, v = tuple(rearrange(qkv, 'b t (d k) -> k b t d ', k=3))
# Resulting shape: [batch, tokens, tokens]
scaled_dot_prod = torch.einsum('b i d , b j d -> b i j', q, k) * self.scale_factor
if mask is not None:
assert mask.shape == scaled_dot_prod.shape[1:]
scaled_dot_prod = scaled_dot_prod.masked_fill(mask, -np.inf)
attention = torch.softmax(scaled_dot_prod, dim=-1)
return torch.einsum('b i j , b j d -> b i d', attention, v)MHA
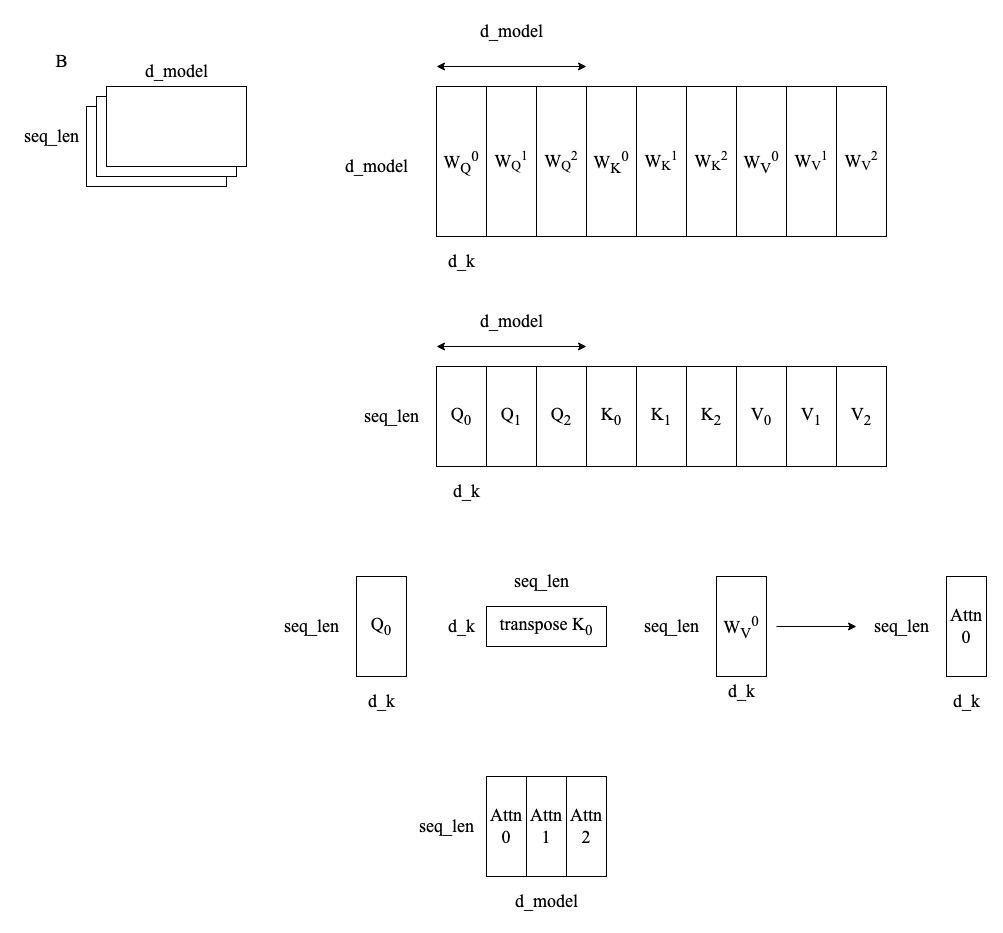
\(MultiHead(Q, K, V) = Concat(head_1, \cdots, head_h) W_{o}\)
\(\text{ where } head_{i} = Attention(X W_{i}^{Q}, X W_{i}^{K}, X W_{i}^{V}) = Attention(Q_i, K_i, V_i)\)
在多头注意力中,训练时会计算出更多的参数,用于表示不同的投影子空间。 但是在非多头注意力中,W 中只有一个投影子空间,所以捕获的特征更少。
class MultiHeadSelfAttentionAISummer(nn.Module):
def __init__(self, dim, heads=8, dim_head=None):
"""
Implementation of multi-head attention layer of the original transformer model.
einsum and einops.rearrange is used whenever possible
Args:
dim: token's dimension, i.e. word embedding vector size
heads: the number of distinct representations to learn
dim_head: the dim of the head. In general dim_head<dim.
However, it may not necessary be (dim/heads)
"""
super().__init__()
self.dim_head = (int(dim / heads)) if dim_head is None else dim_head
_dim = self.dim_head * heads
self.heads = heads
self.to_qvk = nn.Linear(dim, _dim * 3, bias=False)
self.W_0 = nn.Linear( _dim, dim, bias=False)
self.scale_factor = self.dim_head ** -0.5
def forward(self, x, mask=None):
assert x.dim() == 3
qkv = self.to_qvk(x) # [batch, tokens, dim*3*heads ]
# decomposition to q,v,k and cast to tuple
# the resulted shape before casting to tuple will be:
# [3, batch, heads, tokens, dim_head]
q, k, v = tuple(rearrange(qkv, 'b t (d k h) -> k b h t d ', k=3, h=self.heads))
# resulted shape will be: [batch, heads, tokens, tokens]
scaled_dot_prod = torch.einsum('b h i d , b h j d -> b h i j', q, k) * self.scale_factor
if mask is not None:
assert mask.shape == scaled_dot_prod.shape[2:]
scaled_dot_prod = scaled_dot_prod.masked_fill(mask, -np.inf)
attention = torch.softmax(scaled_dot_prod, dim=-1)
out = torch.einsum('b h i j , b h j d -> b h i d', attention, v)
out = rearrange(out, "b h t d -> b t (h d)")
return self.W_0(out)Intuition