所以激活函数的作用是 打破线性性，引入非线性，使神经网络可以：

• 拟合任意复杂的函数（通用近似能力）
• 表达分类边界、抽象特征、决策逻辑等复杂结构

ReLU

\[ \text{FF}(x) = \text{ReLU}(xW_1)W_2 \]

\[ \text{ReLU}(x) := \max(0, x) \]

原始 Transformer 使用的前馈激活函数就是 ReLU。

GeLU

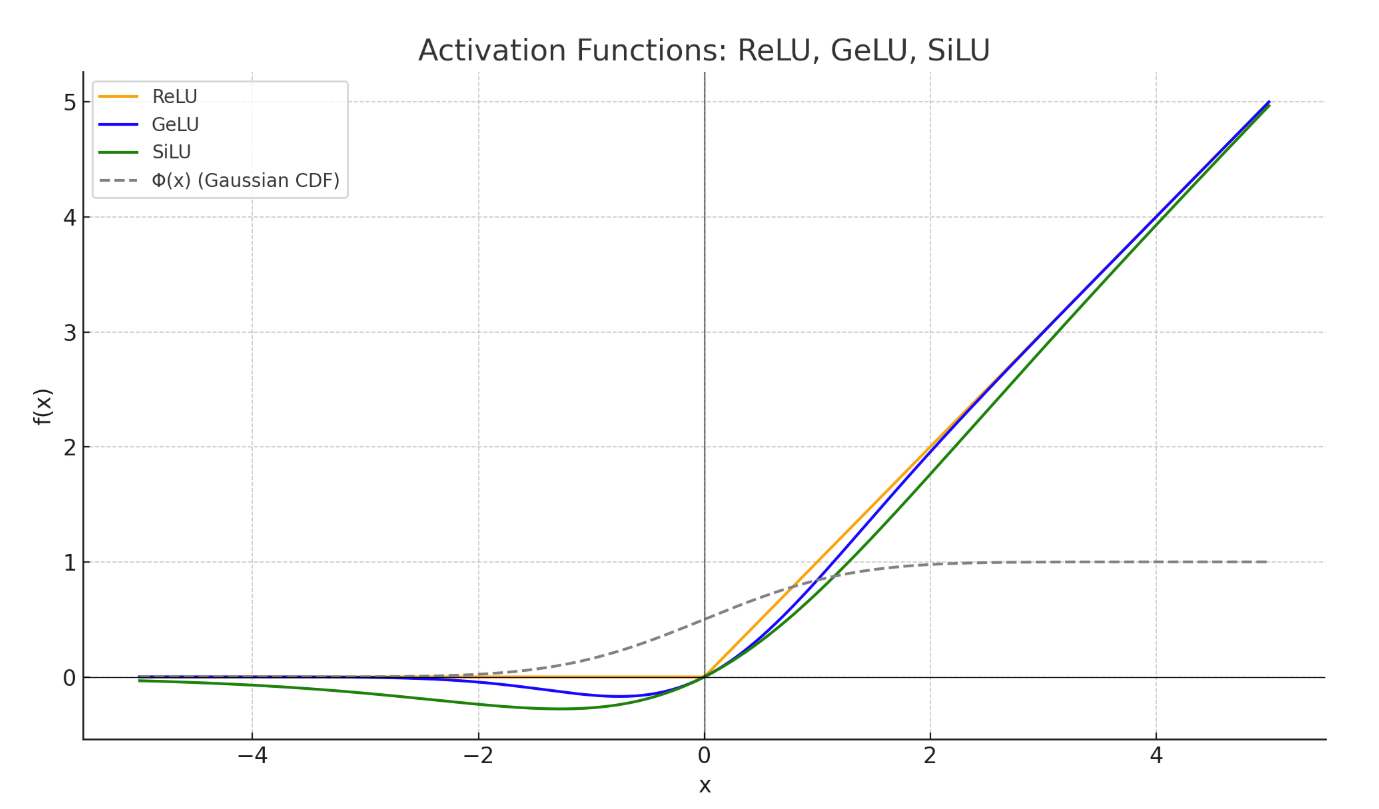
\[FF(x) = \mathrm{GELU}(xW_1)W_2\]

\[\mathrm{GELU}(x) := x \, \Phi(x)\]

这里的 \(\Phi(x)\) 是 标准正态分布的累积分布函数（CDF），也叫高斯误差函数的一种形式。

\[ \Phi(x) := \int_{-\infty}^{x} \frac{1}{\sqrt{2\pi}} e^{-t^2/2} \, dt \]

这是一个 S 形的平滑函数，表示「一个标准正态分布随机变量小于等于 \(x\) 的概率」。

GeLU 的直观理解

GeLU 的激活函数可以理解为：对每个输入 \(x\)，按概率 \(\Phi(x)\) 部分保留它的值。

• \(x < 0\) 时，\(\Phi(x) < 0.5\)，输出被削弱；
• \(x > 0\) 时，\(\Phi(x) > 0.5\)，输出更接近 \(x\)；
• 整体是一种 平滑的门控机制。

常用近似（用于实际计算）：

为了加速计算，GeLU 经常使用以下近似形式：

\[ \mathrm{GeLU}(x) \approx 0.5 x \left(1 + \tanh\left[\sqrt{\frac{2}{\pi}} \left(x + 0.044715x^3\right)\right]\right) \]

这个近似非常精确，且可快速计算，广泛用于 BERT、GPT 等模型。

GPT 1/2/3

SiLU

\[\text{FF}(x) = \text{SiLU}(xW_1)W_2\]

\[\text{SiLU}(x) = x \cdot \sigma(x) = \frac{x}{1 + e^{-x}}\]

Gated Variants

GLU

GLUs (Gated Linear Unit) modify the “first part” of a FF layer:

\[FF(x) = \max(0, xW_1) W_2\]

Instead of a linear + ReLU, argument the above with an (elementwise) linear term

\[\max(0, xW_1) \rightarrow \max(0, xW_1) \otimes (xV)\]

This gives the gated variant (ReGLU) - note that we have an extra parameter (V)

\[FF_{\text{ReGLU}}(x) = (\max(0, xW_1) \otimes xV) W_2\]

GeGLU

\[FFN_{\text{GeGLU}}(x, W, V, W_2) = (\text{GELU}(xW) \otimes xV)W_2\]

SwiGLU

\[FFN_{\text{SwiGLU}}(x, W, V, W_2) = (\text{Swish}_1(xW) \otimes xV)W_2\]